
Симметрия в природе и как человек берет оттуда вдохновение
Ни для кого не секрет, что природа стремится к симметрии и гармонии.
Данная естественная симметричность заложена строением клеток и научным порядком, который возможно объяснить математически. Симметрия является формулой строения клеток. Она служит как чертеж, подсказывая как в идеале, например, цветок должен расти и размещать лепестки. Одни из основных фомрул-систем, которые поясняют данное понятие с математической точки зрения являются L-системы, которые были введены и разработаны в 1968 году Аристидом Линденмайером, венгерским биологом-теоретиком и ботаником из Утрехтского университета.
Как работает симметрия и почему возникает
В этой главе я часто буду ссылаться на информацию из книги Алгоритмическая красота растений (The Algorithmic Beauty of Plants; Аристид Линденмайер и Пшемыслав Прусинкевич), затрагивающую симметрию в математическом понятии, не уходя слишком глубоко в приведенные формулы, затронув лишь теорию и основу.
Системы Линденмайера, или же L-системы, были задуманы как математическая теория развития растений. Первоначально они не включали достаточно подробностей для комплексного моделирования высших растений. Акцент делался на топологии растения, то есть на отношениях соседства между клетками или более крупными модулями растения. Их геометрические аспекты выходили за рамки теории. Впоследствии было предложено несколько геометрических интерпретаций L-систем с целью превращения их в универсальный инструмент для моделирования растений.
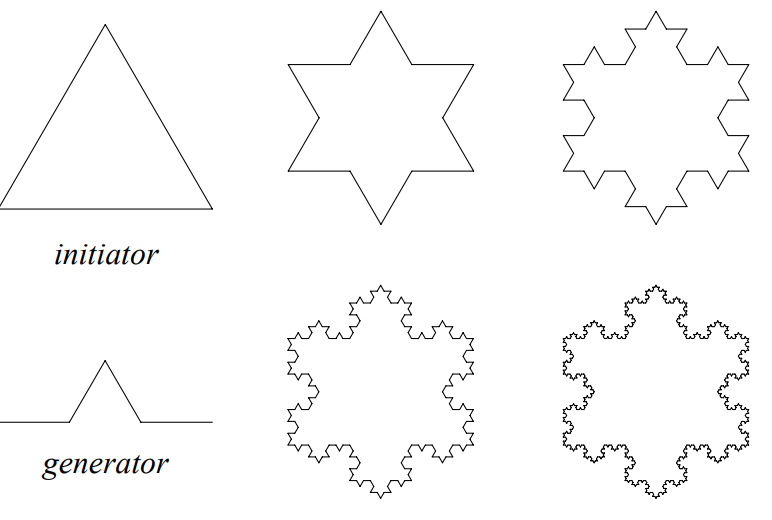
Кривые снежинки (The Algorithmic Beauty of Plants; Аристид Линденмайер и Пшемыслав Прусинкевич)
Такие странные Кривые-снежинки, официальное название данной схемы выше, были предложены в 1905 году Кохом фон Кохом, которую потом переформулирует Мандельброт, подробнее дав им описание:
«Конструкция начинается с двух фигур: инициатора и генератора. Последний представляет собой ориентированную ломаную линию, состоящую из N равных сторон длиной r. Таким образом, каждый этап построения начинается с ломаной линии и состоит в замене каждого прямого отрезка копией генератора, уменьшенной и смещенной так, чтобы иметь тот же концe.» — The Algorithmic Beauty of Plants; Аристид Линденмайер и Пшемыслав Прусинкевич
Не уходя глубоко в математику, данный принцип это все, что нам пригодится при понимании зацикленности строения клеток и генерации, выбора, расположения частей растений. Расположение не хаотично, а циклично.
Видоизмененные соцветия: [a] колос, [b] початок, [с] головка.
Виды симметрии
Осевая симметрия
Пример осевой симметрии
Центральная
Пример центральной симметрии
Вращательная
Пример вращательной симметрии
Скользящая
Пример вращательной симметрии
Нас в основном будут интересовать осевая, центральная/зеркальная симметрии и ее отсутствие. В ботанике мы сможем увидеть и скользящую симметрию, например, в расположении листьев на стебле растений.



